Introduction
This is the excerpt of a report that I submitted in November 1994 as part of a post-graduate university course on Advanced Algorithms and Data Structures.
This is far more academically geeky than most posts on this blog. It may not be of interest to the lay reader.
I have migrated from LaTeX to HTML. I seem unable to locate my original bibliography, leaving the state of my reference section woefully inadequate.
Background
Section, where I explain that this topic is about the “diff” command and was motivated by this war story, ellided.
Practical Applications
The string comparison problem is prompted by many practical applications.
Patch/Version Control
When successive versions of a program are stored or distributed, often relatively small areas of the code have been changed. By producing a “delta” file, it is possible to deliver only the changes, and not a full-copy of the new file.
Programming Tool
It is often useful to compare two documents to see their similarities and differences, including comparing actual output of a program to its desired output for debugging purposes, or for achieving informal version control.
Molecular Biology
The strings are not restricted to ASCII characters. The strings representing the nucleic acid sequences of two strands of DNA can be compared to establish the amount, and location, of evolutionary change.
Screen Updates
Many display terminals offer facilities to applications to manipulate on-screen text. These operations might including deleting lines, or copying text from one section of the screen to another. With program editors, and similar programs which update text on a full screen, it is preferable to take advantage of these terminal facilities as they are often faster, and take less band-width, than a full refresh of the affected areas.
It is necessary to rapidly compare the actual screen and the desired screen, and derive the optimal changes required to make the update.
Shortest Edit Distance
The Problem
The basic string comparison problem is defined below.
Let the u and v be two sequences over an alphabet of symbols, A. These sequences are commonly known as words or strings. The ith element of a sequence is represented by an index, for example, u[i].
With a number of simple operations, it is possible to convert the sequence u to the sequence v.
Basic-Operations
Generally, the allowed operations are :
- Insert; Insert a new symbol into the sequence
uat the positioni. - Delete; Delete the symbol at the position
ifrom the sequenceu.
These operations should be considered to occur simultaneously; all references to positions in the sequence are taken before any modification to the symbol is made.
The minimum number of operations required to convert u into v is known as the shortest edit distance, d.
It is generally possible to simply delete every symbol in u and add every symbol in v, hence d ≤ |u| + |v|, where |u| and |v| are the lengths of the strings u and v respectively.
The basic task to find the set of operations which lead to the shortest edit distance between two strings.
It should be noted that there are many variations in the terminology and choice of identifiers in the literature. However, I have attempted to remain consistent throughout this document.
Introduction to Variations on the Problem
The base problem, described in the previous section, has been adapted by many authors for particular tasks. A section below discusses many of the variations, with justifications for the changes. However, an understanding of a few of the common variations aids understanding of the general algorithms which can solve both the base problem and some variations. Therefore, some of the variations are introduced briefly below.
Finite vs. Unbounded Alphabets
The number of symbols may be limited to a finite number, or it may be unbounded. While many algorithms can handle an unbounded alphabet, some iterate through every possible symbol, and hence must restrict the alphabet’s range.
Weights
The measure for minimum edit distance can be generalised from a simple count of the number of operations to a more complex cost function. Each operation (such as Delete or Insert) may have a separate weight to make some operations preferable to others.
Additional Operations
Insert and Delete need not be the only possible operations; depending on the application, more sophisticated operations might be added.
A common example is Replace; substituting a single symbol with another one. Being able to Transpose a long consecutive sequence of symbols from one string to another can significantly reduce the number of operations required.
Longest Common Subsequence
A subsequence of a word is a sequence of symbols which occur in the word in the same order. The symbols are not necessarily consecutive. Hence aabcb is one example of a subsequence of the string abcabcabc. Finding the longest common subsequence of two strings is the basis of several naïve shortest edit distance algorithms.
Algorithms using the Matrix, D
Several string comparison algorithms build on the same data structure; a matrix of partial solutions.
I introduce this concept below, and then show a few implementations which use it to solve the problem.
Consider an matrix, D, where each element, D[i,j], contains the smallest edit distance between the first i symbols of string u and the first j symbols of string v. The allowed operations include only insertion and deletion.
An example of such a matrix, D, is presented below, to transform the string myers to the string miller, where each symbol represents one character. The method used to calculate each element is described in the next section.
| m | i | l | l | e | r | ||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| m | 1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 1 | 2 | 3 | 4 | 5 | 6 |
| e | 3 | 2 | 3 | 4 | 5 | 4 | 5 |
| r | 4 | 3 | 4 | 5 | 6 | 5 | 4 |
| s | 5 | 4 | 5 | 6 | 7 | 6 | 5 |
The blue element has been highlighted as an example. This element represents the minimum edit distance between the string mye and the string mille, and has a value of 4. The set of 4 operations are listed further below.
The unlabelled top row and the left column of the matrix represent comparisons with an empty string.
Each element also has associated with it the set of edit operations required to perform this transformation within the minimum edit distance. This set might not be unique, and need not be explicitly stored in the table. It can be derived by following a “minimising path” (described below) back to the top left corner.
A minimising path on a D matrix is one which at a given element travels up, left or diagonally up-and-left to the minimum of its “preceding” neighbours. If more than one neighbour has an equal value, the choice is arbitrary. The path continues until it reaches the top left corner.
If the path travels from an element D[i,j] to its left neighbour, D[i,j-1], this represents the insertion of a symbol v[j] in the string u at position i.
If the path travels from an element D[i,j] to its neighbour above it, D[i-1,j], this represents the deletion of a symbol from the string u at position i.
If the path travels from an element D[i,j] to its upper-left neighbour, D[i-1,j-1], and u[i] = v[j], then this means that the two strings match at this point, and no operation is required. As character replacement (as opposed to deletion and insertion) is not allowed in this model, the path may not travel to the upper-left neighbour if u[i] ≠ v[j]. More sophisticated models may allow this move. This is discussed below.
Using the example of the blue highlighted element in the above grid, and the given minimising path (which is only one of many possible equivalent paths) indicated by the bolded digits, we get the following set of operations :
- Add an
iafter them - Add an
lafter theiinserted in the previous step. - Add another
lafter the lastl. - Delete the
y.
Note that the operations should be parallel, and not dependent on previous operations, but they have been ordered here for clarity.
By ordering the operations in the edit set based on the position of the symbols affected, it is possible to see that, for a given solution to the problem, a minimising path through the matrix can always be plotted. Also, all minimising paths lead to correct solutions. These properties have been proven by a number of papers cited in (Ukkonen85).
Deriving a Formula for D
Given that the minimum set of edit operations at a given element can always be derived from one of the three “preceding nodes” (i.e. the neighbouring nodes above, to the left and to the upper-left) by the addition by a single operation (or possibly no operation at all, if u[i]=v[j]), a recursive formula for each element can be generated.
i>0 ⇒
D[i,0]=i
j≥0 ⇒
D[0,j]=j
i,j>0 ∧ u[i]=v[j] ⇒
D[i,j] = min(D[i-1,j]+1, D[i,j-1]+1, D[i-1,j-1])
i,j>0 ∧ u[i]≠v[j] ⇒
D[i,j] = min(D[i-1,j]+1, D[i,j-1]+1)
An O(|u|.|v|) Algorithm
Given this definition of D, it is possible to write a simple algorithm which calculates every element in the matrix. It can be calculated in one pass, moving left to right, top to bottom. Each element’s calculation could be done in constant time. Thus, the total time to compute this is O(|u|.|v|).
When the entire matrix has been computed, the minimising path could be traced back. The length of the path is bounded by |u| + |v|, and the time taken at each point to compute a previous point in the graph is constant.
Therefore, an algorithm could be written to calculate the smallest set of operations to convert a string u into a string v with a time complexity of O(|u|.|v|+|u|+|v|), which simplifies to O(|u|.|v|). The space complexity is O(|u|.|v|); the entire matrix is stored.
(Ukkonen85) claims that this basic algorithm has been invented and analysed several times. While it is algorithmically simple and relatively inefficient for most problems, it has some interesting qualities. Its complexity is not related to the number of symbol matches nor the number of differences between the two sequences. Neither is it dependent on the size of the alphabet, |A|. Also, if the problem is simplified to finding the value of d, without the set of edit steps, the space complexity can be easily reduced to O(min(|u| + |v|)) by storing only the single last computed row or column of the matrix.
An O(|u|.max(1,|u|/log|v|)) Algorithm
Masek and Paterson (Masek80) produced an optimisation of the algorithm by splitting the matrix into precalculated submatrices.
Their algorithm has a few restrictions. The alphabet of symbols, A, must be finite (see below for further discussion). The weights or costs of each operation (see below) also have a minor restriction. They must be integral multiples of a single positive real.
In an example from (Masek80), the string babaaa is compared with ababbb over an alphabet, A = {a, b}.
The full D matrix for this comparison would appear like so:
| b | a | b | a | b | b | ||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| a | 1 | 2 | 1 | 2 | 3 | 4 | 5 |
| b | 2 | 1 | 2 | 1 | 2 | 3 | 4 |
| a | 3 | 2 | 1 | 2 | 1 | 2 | 3 |
| b | 4 | 3 | 2 | 1 | 2 | 3 | 4 |
| b | 5 | 4 | 3 | 2 | 3 | 4 | 5 |
| b | 6 | 5 | 4 | 3 | 4 | 5 | 6 |
However, rather than calculate every value in the matrix, they split it into precalculated matrices of size m + 1 which can be retrieved from storage. The D matrix is padded if necessary to ensure that its length and width is evenly divisible by the submatrices.
If m had the value of 3, the matrix D from above would be divided into submatrices of length and width 4 :
| b | a | b | a | b | b | ||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| a | 1 | 2 | 5 | ||||
| b | 2 | 1 | 4 | ||||
| a | 3 | 2 | 1 | 2 | 1 | 2 | 3 |
| b | 4 | 1 | 4 | ||||
| b | 5 | 2 | 5 | ||||
| b | 6 | 5 | 4 | 3 | 4 | 5 | 6 |
The blank elements need not be calculated, leading to a significant time saving.
The cost penalty is in storage requirements and in the time taken to precalculate the submatrices. Although there are some basic optimisations, the time complexity for the precalculations is O(km) where k is dependent on |A| but not on m nor the strings being compared.
By selecting m = floor(logk |u|), we get an effective time complexity of the matrix precalculations of O(|u|).
The time complexity of the entire string comparison algorithm, including the matrix precalculation, the generation of D, and a computation of the minimum path has, depending on the optimisation method chosen, a time complexity of O(max(|u|)) and a space complexity of O(sqrt(|u|).log(|u|)) or a linear time complexity and a space complexity of O(|u|2/log(|u|)).
An O((|u|+|v|).d) Algorithm
The following algorithm was independently discovered by Ukkonen (Ukkonen85) and by Miller and Myers (Miller85). Myers gives a more rigorous examination of the algorithm in (Myers86), but (Miller85) is probably the most readable description.
The algorithm focuses on the comparison of text files; the algorithm is not dependent on the size of the alphabet, which may be unbounded. It is, however, dependent on the number of differences between the two sequences of symbols, i.e., d. With comparisons of program files, it is common for the size of d to be relatively small.
This algorithm is an optimisation of the basic algorithm described above. The basic algorithm suffers from inefficiently computing a large number of elements which are never visited by the minimizing path. This optimization aims to reduce the amount of computation by restricting the number of elements that need to be computed.
In order to understand how the simplification is done, it is necessary to appreciate that the matrix, D, has a strict structure. In particular, the diagonals have some important features.
Each element in the matrix belongs to a single (negative gradient) diagonal. The diagonal number of D[i,j] is defined to be j-i.
Each diagonal is labelled in the matrix below. Note that this matrix does not contain the values of D, but instead each field holds the diagonal number. This is a 4×5 matrix, with 0≤i≤3 and 0≤j≤4, and can therefore be used to compare a string of length 3 with a string of length 4.
| 0 | 1 | 2 | 3 | 4 |
| -1 | 0 | 1 | 2 | 3 |
| -2 | -1 | 0 | 1 | 2 |
| -3 | -2 | -1 | 0 | 1 |
In a D matrix representing the minimum edit distances between two strings, the following properties hold:
- Travelling down a diagonal, the values are always monotonically increasing. That is,
D[i,j] ≥ D[i-1, j-1], ∀ i,j>1. - Travelling down a diagonal, increments are always either 0 or 2. That is,
(D[i,j] = D[i-1, j-1]) ∨ (D[i,j] = D[i-1, j-1] + 2) ∀ i,j>1. - Diagonal
khas an leftmost value of|k|. Hence, all of its values are of the form|k|+2cwherecis a natural number. - All the elements with a given value of [[d lie on the diagonals
-d,-d+2, …,d-2,d.
Using these properties, Ukkonen, and Miller and Myers, determined that it was not necessary to generate every value in the matrix. Instead, it was possible to calculate only those elements with a minimum edit distance of less than or equal to the final minimum edit distance.
First, all cells in the matrix with the value of 0 are filled in. Then all the cells in the matrix with the value of 1 are filled in, and so on. This is re-iterated, until the bottom-most cell is filled in. At this stage, the minimum edit distance of the two sequences has been found, and the algorithm can stop.
The method for filling each value in the matrix, as described in (Miller85), is a three step process. Suppose the process is attempting to fill in the value e > 0. That is, every element with the value of e should be filled in by the end of the three steps.
- Move Right: First, any unfilled cell to the right of a cell containing
e-1is filled in with the valuee. The appropriate insertion operation is added to the associated editing steps. - Move Down: Second, any unfilled cell below a cell containing
e-1is filled in with the valuee. The appropriate deletion operation is added to the associated editing steps. - Slide down the Diagonal: Finally, for every value of
ethat has been added at a positionD[i-1,j-1], if a diagonal step is permitted (i.e.u[i] = v[j]), thenD[i,j]is set tolas well. This step is repeated on the newly set value. This represents a match in the symbols between the two strings, and no extra edit operation is required.
The matrix must be initialised by running the “Slide down the Diagonal” step on the 0 value at D[0,0] before the loop starts. The above three steps are applied iteratively until the bottom-right hand corner value is filled in.
This algorithm is best illustrated through an example. To show the potential time savings, two similar strings have been chosen, appropriate and approximate.
The following matrix indicates the state of D after the 0 values have been initialised.
| a | p | p | r | o | p | r | i | a | t | e | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | ||||||||||||
| a | 0 | |||||||||||
| p | 0 | |||||||||||
| p | 0 | |||||||||||
| r | 0 | |||||||||||
| o | 0 | |||||||||||
| x | ||||||||||||
| i | ||||||||||||
| m | ||||||||||||
| a | ||||||||||||
| t | ||||||||||||
| e |
After the first “Move Right” step, we have the following matrix.
| a | p | p | r | o | p | r | i | a | t | e | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | |||||||||||
| a | 0 | 1 | ||||||||||
| p | 0 | 1 | ||||||||||
| p | 0 | 1 | ||||||||||
| r | 0 | 1 | ||||||||||
| o | 0 | 1 | ||||||||||
| x | ||||||||||||
| i | ||||||||||||
| m | ||||||||||||
| a | ||||||||||||
| t | ||||||||||||
| e |
The first “Move Down” step has a similar effect to the matrix, but the diagonal slide has no effect at this stage.
| a | p | p | r | o | p | r | i | a | t | e | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | |||||||||||
| a | 1 | 0 | 1 | |||||||||
| p | 1 | 0 | 1 | |||||||||
| p | 1 | 0 | 1 | |||||||||
| r | 1 | 0 | 1 | |||||||||
| o | 1 | 0 | 1 | |||||||||
| x | 1 | |||||||||||
| i | ||||||||||||
| m | ||||||||||||
| a | ||||||||||||
| t | ||||||||||||
| e |
This completes the insertion of the 1 values in the table.
The 2 values are now added using the same three steps. Once again, the diagonal slide has no effect.
| a | p | p | r | o | p | r | i | a | t | e | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | ||||||||||
| a | 1 | 0 | 1 | 2 | ||||||||
| p | 2 | 1 | 0 | 1 | 2 | |||||||
| p | 2 | 1 | 0 | 1 | 2 | |||||||
| r | 2 | 1 | 0 | 1 | 2 | |||||||
| o | 2 | 1 | 0 | 1 | 2 | |||||||
| x | 2 | 1 | 2 | |||||||||
| i | 2 | |||||||||||
| m | ||||||||||||
| a | ||||||||||||
| t | ||||||||||||
| e |
The next value inserted into the table is 3. This time, however, the diagonal slide allows the bolded 3 to be added.
| a | p | p | r | o | p | r | i | a | t | e | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | |||||||||
| a | 1 | 0 | 1 | 2 | 3 | |||||||
| p | 2 | 1 | 0 | 1 | 2 | 3 | ||||||
| p | 3 | 2 | 1 | 0 | 1 | 2 | 3 | |||||
| r | 3 | 2 | 1 | 0 | 1 | 2 | 3 | |||||
| o | 3 | 2 | 1 | 0 | 1 | 2 | 3 | |||||
| x | 3 | 2 | 1 | 2 | 3 | |||||||
| i | 3 | 2 | 3 | 3 | ||||||||
| m | 3 | |||||||||||
| a | ||||||||||||
| t | ||||||||||||
| e |
4 is now inserted into the table. In this iteration, the diagonal slide travels far enough to reach the bottom corner.
| a | p | p | r | o | p | r | i | a | t | e | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||||||||
| a | 1 | 0 | 1 | 2 | 3 | 4 | ||||||
| p | 2 | 1 | 0 | 1 | 2 | 3 | 4 | |||||
| p | 3 | 2 | 1 | 0 | 1 | 2 | 3 | 4 | ||||
| r | 4 | 3 | 2 | 1 | 0 | 1 | 2 | 3 | 4 | |||
| o | 4 | 3 | 2 | 1 | 0 | 1 | 2 | 3 | 4 | |||
| x | 4 | 3 | 2 | 1 | 2 | 3 | 4 | |||||
| i | 4 | 3 | 2 | 3 | 4 | 3 | 4 | |||||
| m | 4 | 3 | 4 | 4 | ||||||||
| a | 4 | |||||||||||
| t | 4 | |||||||||||
| e | 4 |
At this point the algorithm terminates. The set of editing steps can be found by following one of the minimizing paths back; one such path has been bolded.
In the example above, a significant portion of the matrix was not evaluated. This algorithm tends to be more efficient with the inputs in which there are few differences. It has been shown (Miller85, Ukkonen85 and Myers86) that this algorithm is O((|u|+|v|).d). In its worst case, however, the entire matrix must be evaluated, and the algorithm resorts to O(|u|.|v|).
With a refinement, which is described in (Myers86), the expected time complexity can be reduced to O(|u|+|v|+d2) and the worst-case time complexity can be reduced to O(|u|.log|u|+d2). The space complexity of the refinement is only O(|u|+|v|).
Block Moves
Tichy (Tichy84) provides a simple algorithm, and two enhancements, which achieve some impressive results. The algorithms do not use the D matrix from the previous sections, but instead are based on the longest common prefix of the two strings.
Tichy does, however, use a different set of allowed operations. Rather than use a set of operations which apply in parallel to a string to transform it into another string, he uses just two operations to construct a new string from scratch, by either copying parts of the old string, or appending a new string to the end. With this method, there is no requirement for a delete operation; an unnecessary character from u is just never copied across to v.
The two allowed operations are :
- Insert: The Insert operation here allows a symbol to be appended to the end of the target string,
v. It is only used for symbols which appear in the target string,v, but which do not appear anywhere in the source stringu. - Block Move: Perhaps better titled “Copy”, the Move operation takes a specified consecutive sequence of symbols from
uand appends it to the end ofv. The Move operation may be applied to a particular sequence of the source string more than once.
The insert operations for a given pair of strings u and v are fixed; any symbol in v which is not in u has an insert operation corresponding to it. No other symbols are inserted in v; they are moved from u. Thus an algorithm which minimises the number of move operations effectively minimises the edit distance.
The different paradigm for the edit operations (constructing a new string versus transforming a string) means that a single pass edit is (generally) no longer possible. The paper does, however, explain how it is still possible to perform in-place transformations.
An O(|u|.|v|) Algorithm
Tichy’s basic algorithm is very simple.
The algorithm starts at the first symbol in v and iterates through all of u looking for the longest sequence of characters matching the prefix of v. If none exist, an insert operation to add the symbol to v is added to the sequence of edit operations. Otherwise, a move operation, which copies the longest found string is added to the sequence of edit operations.
Before the loop is repeated, the prefix is removed from the target string.
When the target string has been completely consumed the algorithm is complete.
Tichy proves that this finds a smallest sequence of edit operations.
In the worst case, all of v must be iterated through. Each iteration of v involves a linear search through u, so the time complexity is O(|u|.|v|). There are no sophisticated data structures in this version and the amount of space required is minimal; it is O(|u|+|v|).
An O(|u|.|v|/|A|) Algorithm
A simple improvement of the algorithm can make a significant difference when there is little replication of symbols; that is, when the size of the (used) alphabet |A| is close to the size of the source string.
The basic algorithm does a linear search through u for the prefix of v. This can be optimised by preparing an index for each symbol with a list of occurrences of that symbol in u. The time taken for the production of the index is linear and the estimated overall run time of the algorithm is O(|u|.|v|/|A|). When |A| approaches |u|, the time complexity approaches linear.
The space complexity is not changed; the index or hash table can be stored in O(|u|+|v|).
A linear time and space algorithm
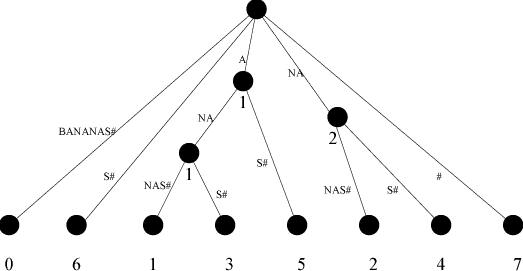
Tichy’s second improvement improves the time complexity further by improving the behaviour of the index data structure; a unique character, #, is appended to the source string u and a “suffix tree” is created from it.
Each edge in a suffix tree is labelled with a sequence of symbols. There is a leaf node for every possible suffix, of which there are |u|, and the path from the root to a leaf node spells out the suffix.
If two suffixes share a common prefix, there is an interior node to which they are (possibly indirectly) attached. The path from the root node to this interior node spells out this suffix.
An example of a suffix-tree is presented in the figure below:
|
The suffix tree can be used to match a pattern in time proportional to its length, by following the appropriate edges until the prefix no longer matches any path, and using the value associated with the last node reached. Tichy claims it can constructed in a space and time proportional to |u|.
I think the reference to “last node reached”, means that if you only match the first letter of the string associated with the edge, you still navigate down it to find the starting point of the matching string, but go no further.
Using a suffix tree, the overall algorithm achieves a time and space complexity of O(|u|+|v|). The constant factor is poorer than the algorithm described in the previous section. Experimental results achieved by Tichy suggest that, in practice, the suffix tree does not outperform the basic index method until the string sizes are well over 1000 symbols long.
Variations on the Problem
There are many variations on the basic shortest edit distance problem. These have often been sparked by the special requirements of particular problem domains.
Molecular Biology is a good example. It has been found that the shortest set of operations transforming one DNA strand to another often does not accurately model the most likely biological transformation (Sankoff92). In order to provide more biologically-feasible results, modifications to the problem definition and the algorithm have been introduced.
Finite vs. Unbounded Alphabets
In some applications, the number of symbols in the alphabet is finite. Notably, in molecular biology applications, the alphabet size is often only 4 (one symbol for amino acid building block in DNA).
Unbounded alphabets are useful for other problems. When comparing computer programs, lines are commonly a useful conceptual level at which to display changes. An English document, however, might be better compared at the (English) word level. With these domains, each “symbol” might be quite complex; it may represent an entire English word or line of text.
Some algorithms’ performances are dependent on the size of the alphabet. These systems cannot be used practically with large alphabets.
Other algorithms’ performances are dependent on the number of potential matches of each symbol to a symbol in the other string. These algorithms generally perform much better on large or unbounded alphabets, due to the smaller number of matches.
With more complex symbols, especially lines of a file, symbol equality functions may be quite slow. It may be more efficient to take a hash value of each line of the file. In this way, hash values can be compared relatively quickly; if they are different, the lines are unequal. If the hash values are the same, then a slower line comparison must be made.
Weights
Different costs may be assigned to different operations. The basic edit distance problem can be considered a special case, in which the weight of each operation is 1 unit.
One purpose for this is to mimic the probability distribution of various different biological operations occurring in an evolutionary environment (Sankoff92, Naor93).
Another possibility is to add extra non-primitive operations. For example, a replace operation (which exchanges one symbol for another) could be added, with a weight which is the sum of the insertion and deletion operations. This makes no difference to the output of the algorithm, but the short-cut operation might improve efficiency.
Where each operation has constant weights, it is possible to use a similar algorithm to the one described above. Slight modifications must be made to the equations.
For example, if w represents the cost of an insertion or a deletion and a replacement operation is allowed, for the sum cost of an insertion and a deletion, the new equation for calculating values of the matrix would be:
i>0 ⇒
D[i,0]=i
j≥0 ⇒
D[0,j]=j
i,j>0 ∧ u[i]=v[j] ⇒
D[i,j] = min(D[i-1,j]+w, D[i,j-1]+w, D[i-1,j-1])
i,j>0 ∧ u[i]≠v[j] ⇒
D[i,j] = min(D[i-1,j]+w, D[i,j-1]+w, D[i=1,j-1]+2w)
The rest of this section was “commented out” of my final report. I don’t recall why; it seems like a good idea to me now:
Although none of the literature I have investigated discusses it, I anticipate that it could also be used to favour consecutive operations and, hopefully, produce more natural edit operations for human understanding.
To illustrate this point, consider the operations required to convert the string A kilogram of cheap lead! into the string A kilogram of solid gold!. In the following examples, conversions have been indicated by marking deletions with strikeout letters and insertions with the bolded letters. The shortest edit distance with the basic weighting of 1 unit per operation would lead to the following transformation: A kilogram of solid However, by applying a weight function it may be possible to favour consecutive runs of the same operation; hence we might get the more intuitive transformation : cheap golead!A kilogram of cheap leadsolid gold!
Such a weight function will almost certainly make the algorithm more complex. However, the transformations are likely to be more understandable for human readers.
Additional Operations
As well as using the Insert and Delete operations described in above, it is possible to define additional operations.
A paper by Sankoff (Sankoff92) is a good example of how adding extra operations can provide a more useful system.
Sankoff compares biological structures at a higher structural level than nucleotide sequences. Rather than an alphabet consisting of 4 different nucleotides, Sankoff compares sequences of genes.
Each gene is sufficiently complex that effectively every symbol in the sequence is unique; the alphabet is unbounded.
Sankoff also suggests some more operations which are biologically feasible:
- Inversion: An arbitrary length of the sequence can have each of its symbols placed in the reverse order.
- Transposition: A consecutive sequence of symbols may be removed from one section, and inserted at another point.
- Sequence Deletion: Entire lengths of the sequence may be deleted with one operation.
- Reciprocal Translocation: Two complementary transpositions, substituting one section of the sequence for another, may occur.
- Duplication: An entire gene may be copied to another section of the sequence.
Although these operations are far more complex than the basic operations, Sankoff argues that they are more evolutionarily relevant.
The issue of weights are discussed, and Sankoff refers to experimental data to justify the emphasis of some operations over others.
DERANGE, the program described in the paper to find the edit distance, is algorithmically uninteresting. It uses a limited branch-and-bound search, and while the space and time complexity is not discussed formally, it is noted that as the problem becomes more complex (i.e. the sequences become larger), it soons becomes impractical to perform an exhaustive search.
Another application in which operations might be added is for the screen update problem. The operations considered should match those provided by the terminal, which might include line delete or scrolling operations.
Longest Common Subsequence
Finding the longest common subsequence between two strings is a separate problem to the shortest edit distance issue. Myers (Myers86) argues that they can be solved by the same technique.
Consider the minimising path described above. The horizontal and vertical lines represent the set of edit operations required to perform a transformation between the two strings. The set of diagonal lines represent matches between the two strings; the parts of the longest common subsequence. The total number of diagonal links in the path is the length of the longest common subsequence.
Searching for Non-optimal Solutions
Naor and Brutlag (Naor93) claim that no simple method to obtain the shortest edit distance and no set of existing weights has proven to be satisfactory for biological applications. There is no evidence that the shortest edit distance is a good approximation to the likely manipulations found in nature.
Their solution is to produce an algorithm that generates a number of near-optimal results, which can be examined by hand. They also construct a system of “canonical” solutions, which can be combined to produce any sub-optimal solution. In this way the number of sub-optimal solutions presented can be reduced to a few important distinctions.
A method or representing the various solutions is also provided, to enable different results to be conveniently examined.
Approximate String Matching
Another variation to the basic edit distance problem is to combine it with the basic string matching problem. In this way, a user might search for an approximate string. Any string close to the search key may be detected. This also has uses in applications such as spelling checkers.
Landau and Vishkin (Landau89) present both serial and parallel algorithms to address this issue.
Recognising Sep-Min
Conclusion
The problem of finding the smallest set of operations to transform one string of symbols into another is an important one in several fields. With the potential for very large strings, it is important to find algorithms which have reasonable time and space complexities.
A simple algorithm, independently discovered by two groups, provides an algorithm which works well for files which have few differences. This is generally suitable for many programming tasks, but under worst case conditions has a similar complexity to a very basic algorithm which is O(|u|.|v|).
Using a more sophisticated set of operations including the block move, it is possible to use Tichy’s algorithm which runs in linear time and space, but with a poor constant time.
The basic problem has been extended in many ways, to make it more suitable for particular domains. In particular, molecular biologists use edit distance to compare genetic structures at various levels; the requirements of metrics to calculate the shortest edit distance for DNA are very different to the types used in software engineering.
Ellided mention of the Sep-Min section.
References
Unfortunately, the references were stored in a separate file to the original text; this file has been lost. Apologies to the unknown authors.
- Chang92
- Chan92
- Garel93
- Landau89
- Masek80
- Miller85
- Myers86
- Naor93
- Sankoff92
- Tichy84
- Ukkonen85
Comment by turbo on June 28, 2006
Nice paper. However, in the O((|u|+|v|).d) Algorithm you state the increment going down a diagonal is either 0 or 2, which is incorrect. A simple counter example is the array for the string ‘cat’ and ‘hat’
which is :
xxcat
x0123
h1123
a2212
t3321
Since the edit distance is 1, and the upper left corner is 0, this shows that the increment can be 1. In fact, any pair of strings with edit distance of 1 will exhibit this property.
Comment by Julian on June 28, 2006
Thanks Turbo,
You made me very happy, because your comment was evidence that someone actually read – and understood – the report!
In your grid, it appears that the edit distance between the string
candhis 1.This is only true if you permit the Replace operation (i.e. Replace ‘c’ with ‘h’.) In the analysis of that section, it assumed the only basic operations were Add and Delete (i.e. Delete ‘c’. Add ‘h’.)
I agree that, if you can use Replace as one of the basic operations, then the increment going down the diagonal can either be 0 or 1 (not 2), and the rest of the analysis needs to be appropriately re-jiggered to cover that.
Comment by turbo on July 2, 2006
I have been recently speaking to Dr. Gene Myers. His algorithms are very elegant and fast, however as I found out, and as you clearly realized, they do not allow for substitutions, which is one of the allowed operations of Levenshtein distance.
I have coded up a few versions of code that computes Levenshtein
distance. I wrote the really obvious one, as well as the one dimensional storage version of that. I acutally used that code for many years.
After some gentle encouragement, I searched the internet for better algorithms. I found references to Ukkonen’s work. I optimized my code to only compute the diagonals needed. That sped up my code by roughly a factor of 6. I knew of his other optimization, which computes the cells of the 2d array in order of distance. I also coded that up, however I have not found an efficient way to do so. There are several operations in my code that are O(n^2), which is unfortunate. The algorithm does fill in less values in the 2d array, but it takes much too long. Perhaps I will figure out some very clever, efficient way
to fill out the distances of the array in order…
I also coded up a classic implementation of the Damerau/Levenshtein distance which also allows for transpositition.
Thanks for fixing the typo in my array where I included an extra
value…
If you have access to Ukkonen’s papers, I would really like to see them. They seem to be too old to be online….
turbo
Comment by entY8 on May 24, 2007
Thanks a lot for this; it was the first useful site I found on this topic 😀
(btw, I found it via Google somewhere among the first few hits)
Comment by aj on June 17, 2007
Hi,
How about a minor modification to the diff heuristic such that when one file is a proper subset of the other (meaning on only deletions required), it would, without reducing the efficiency give the best diff?
Please let me know your thoughts on this.
Regards,
Arjun
Comment by Maarten on February 24, 2010
The “Myers86” reference is most likely “An O(ND) Difference Algorithm and Its Variations“, published in 1986 by Eugene W. Myers.
Comment by Jacob on April 9, 2010
Perhaps I am misunderstanding, but it appears to me that the last two rows and columns in the An O(|u|.max(1,|u|/log|v|)) Algorithm are not correct – They indicate an edit distance of 6 for ‘bababb’ vs ‘ababbb’, however I think the distance should be 2 (remove char 1 from string 1 and add ‘b’ to the end of string 1).