OddThinking

I am going to talk about three embodiments of the same paper-and-scissors magic trick, from the downright silly to the impressive to the illegal.

Then I will finish up with some discussion about the policies of the Reserve Bank of Australia.

The Silly

It is not a very good trick, but it demonstrates the basics.

Take some graph paper, and draw 13 parallel lines, like so:

Now take some scissors and cut them diagonally into two parts.

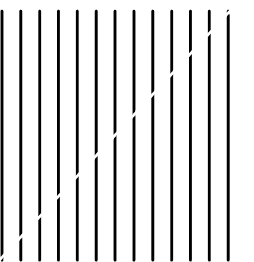
Now shift the bottom piece of paper to the right and up a bit, until each bottom half of the line lines up with the top half of the line to its right. Like so:

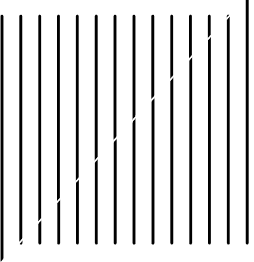
Now count the lines. Wow! Like magic, now there are 14! Where did the extra line come from?

Okay, like I said, not jaw-dropping, but easy to understand.

The Impressive

About 20-25 years ago, there was a neat magic trick published in Scientific American. I cannot reconstruct it here – my drawing skills are nowhere near up to it. But I can give you an idea of what it was like.

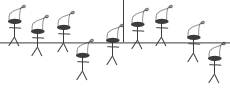
It consisted of three strips of paper, which could be lined up to form a picture of gnomes, on a white background.

The picture below gives you a vague feel for the result. In the real image, there were 13 gnomes (IIRC), each gnome was different (not a clumsy cut-and-paste), and each gnome was an intricate artistic drawing (not a clumsy stick figure).

After inviting the mark to count the gnomes, the top two strips of paper were reversed around so the shorter piece was placed on the left of the longer piece. The drawings had been skillfully layed out so that the gnome tops and bottoms still lined up (unlike my clumsy effort – I made no attempt to achieve this).

Then it was time to count the gnomes again. Astonishingly, there were 14. Where did the extra gnome come from?

I doubt I have adequately conveyed the sense of amazement that was felt here. It really was an impressive little trick. Even when you know how it was done, it was still an applause-worthy feat.

The solution was that each of the 14 gnomes was just a fraction shorter than the original 13. They had been drawn in such a way that the missing pieces were easy to overlook – a hat was a bit shorter, a beard a little bit more compacted, the bobble from the hat or the tip of the shoe was missing. Essentially, it was the same trick as the parallel lines, just executed far more professionally.

The Illegal

Take a wad of 13 large denomination bank notes.

Trim a strip off the right hand edge of the first one. The strip should be only 1/14th the width of the total note. Try to spend the remainder of the note. Most people wouldn’t object to accepting it; it is barely damaged.

From the second note, trim off a strip 2/14ths of a total note wide. Then sticky tape the first strip to the right of the second note. This note will be a bit shorter than normal. Try to spend that note. We’ve all seen notes in circulation that have been ripped and then taped back together. The fact that it is a smidgin shorter isn’t likely to raise any eyebrows.

From the third note, trim off a strip 3/14ths of a total note wide. Get out the sticky tape and repeat.

By the time you get to the end of the 13 original notes, some magic has happened. You have produced a total of 14 notes – each one a little shorter than it should be.

Congratulations – you are now a counterfeiter wanted by the police. In Australia, you have broken the Crimes (Currency) Act of 1981. I am probably breaking some conspiracy law if I recommend doing it, so don’t do it!

Protecting Yourself?

How does the mint protect you from this trick? My understanding used to be that they used the magic of serial numbers.

Each note has two serial numbers – one printed diagonally opposite the other.

I was told that the bank would check before accepting a damaged note that both serial numbers are visible and they match.

So you should be careful of accepting taped-up notes. It the left-hand serial number doesn’t match the right-hand serial number, you should reject it… or should you? I recently found out that this was wrong! (Well, in Australia at least!)

Reserve Bank of Australia Policy

The Reserve Bank of Australia are quite clear about their policy:

The presence or absence of a serial number or other specific feature (e.g. the clear window) is not a determining factor when assessing damaged notes for value.

Instead, the value of a damaged note is based on the percentage of the note that you have that is undamaged. They have special cases for more than 80% damage (nil paid) or less than 20% damage (100% paid).

So you can effectively pay someone $10 with half of a $20 note! But beware! The act of cutting the note in half is still illegal.

Presumably two taped-together mismatching notes will be separated before being valued. That should successfully overcome the counterfeiting trick as described.

So, I learnt something I found interesting; I hope you found it interesting too.

Disclaimers: IANAL. IANA Conspiracist.

[Update: Re-did the first three diagrams to make them make more sense.]