Mike Pope published a little maths puzzle.
The challenge is to calculate every integer value between 0 and 100 using only the number 4.
Rules:
- You may use only the digit 4.
- Important: You may use no more than four 4’s.
- You may use (only) the following operators:
+ (addition)
– (subtraction)
x or * (multiplication)
/ (division)
√ (square root)
! (factorial)- You can combine the operators to create any (otherwise legal) expression. Parentheses are ok.
You can combine the operators to create any (otherwise legal) expression. Parentheses are ok.
Okay, let’s start.
I need to write down 101 answers. That will take a lot of paper and rote work. Why don’t I use a computer to record my progress?
This puzzle is going to take a bit of arithmetic. That’s going to lead to lots of silly mistakes and rote work. That’s clumsy and not fun. Why don’t I get the computer to do the arithmetic?
Using the built-in calculator is just as error prone, and Excel is a bit clumsy for this – too much rote work. Why don’t I throw together a little calculator in Python?
Brackets are clumsy to parse. Let’s use our old friend RPN!
Tappity-tap-tap! Look, I’ve made a stack-based state-machine that handles the operators Four, Add, Substract, Multiply, Divide, Factorial and Square Root. It stores the results on a stack, and each function returns whether there was an error or not. A Result function returns the result when it is required.
Tappity-tap-tap! A simple parser that reads a string and calls the appropriate functions.
The parser reads in a string containing any of the following characters: “4”, “+”, “-“, “*”, “/”, “!” and “R”. (“R” = square root. The √ symbol was causing character-encoding issues I couldn’t be bothered solving.) The parser then calls the appropriate transition on the state-machine.
That leads to ambiguity for “44” – is it forty-four or two fours on the stack. I change the Four operator to remember whether the last operator was a four – if so, multiply it by 10 and add 4. I also add a “,” operator that merely separates fours, so now “44” and “4,4” are distinguishable.
When the parser gets to the end of the string, it returns the result (if it is an integer between 0 and 100) or an error.
Okay, now I can write parse("4,4!+4/") and get 7 – i.e. ((4+(4!))/4) = 7.
I can going through the numbers from 0 to 100 and see if I can come up with some formulae.
Let’s see:
- 4,4- = 0
- 4,4/ = 1
- 4,4+4/ = 2
- 4,4+4+4/ = 3
- 4 = 4
But wait! While I am trying to find these expressions, I keep finding solutions for other numbers by mistake. I may as well record these when I think of them for later. Hold on… that sounds like rote work.
Tappity-tap-tap! Here’s a simple table that records every expression against the result it gives (so long as it is an integer between 0 and 100).
Now, I can blithely guess away – 4!4*4+ = ? – and the computer keeps track of the useful solutions I find along the way.
I may as well enter all the legal one, two and three character expressions to cover quickly cover the answers to 2, 4, 24 and 44.
What about all the four character ones. Takes me a bit longer – there are 21 of them, but now I have covered 12 numbers.
Well, wait a minute. I am doing rote work coming up with legal combinations!
Let’s get Python to generate all the five character strings!
- The first digit may only be a 4.
- The second digit may only be a 4, ‘,’, ! or R.
- The remaining digits can only appear if the preceding characters don’t lead to an error, such as division by zero.
Let’s look at the profile. Ouch, it is all string handling. Let’s improve that. Try again. Tappity-tap-tap. Factorials? Cache them. Tappity-tap-tap. There, that’s much faster!
Now I can just set it going, sit back and watch the results! That’s my way of solving a puzzle!
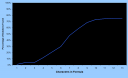
This graph shows how many solutions I found as I increased the total legal length of the formula.
By the time I get to formulae of length 13, I have found 76 of 101 answers, and it is clearly tapering off.
This graph below shows how long each iteration took (wall time, so it isn’t a very good measure – it is affected by what else I was doing on my computer at the same time). Note carefully that it uses a logarithmic scale!
The next iteration is going to take about 16 hours, and is likely to not add many more solutions.
Hmmm… This isn’t going well. It is certainly going to take a long time to find all 101 solutions, and it doesn’t even look like it is going to be soluble. Have I got a bug?
Wait up! Now there is an update to the original post! More operations are permitted!
Exponent? Easy.
Concatenation? I was already supporting that; I had assumed it was legal from context.
Decimal? I add it as a postfix operation “.” that maps 4 to “0.4”, 44 to “0.44” etc. So if I write “444.”, I will get the result 0.444.
Overbar? This is trickier, and takes a bit more thought.
First, let’s represent it as an underscore to save dealing with character-encoding issues!
The only legal case I can see for this operator is directly after “4.” (which is 0.4, based on the new postfix decimal operator. The overbar would turn that into 0.4444…)
My point is that you can’t say “4,4,4+/_” and expect the overbar operator to work out as (4/(4+4)) = 0.5, and then convert that to 0.55555555.
You could use it after “44._”. That would also translate to 0.4444…, but that is longer than “4._” so it isn’t a preferred solution. Let’s just rule it out.
So really, we just need only symbol that can only take a 4 numeral and convert it to 0.4444… So “4_4+” now equals 4/9+4. Done.
This introduces an issue with rounding that I didn’t properly cover before. Is 25.9999… equal to 26? Before the software said no. Now, it accepts it if the epsilon error is less than 10-8.
Let’s start again, with the new rules.

Ooh, the success rate is clearly higher, starting when the formula is five characters in length.
I still haven’t solved it completely, but I am hoping that all is left is the waiting… (It is running much slower – not only do the extra operators introduce more combinations, but exponentiation is slow.)
Expect an update later on the progress of this latest run!

Comment by bjkeefe on August 26, 2007
I’ve always liked this puzzle, ever since I read about it in Martin Gardner’s book, The Amazing Dr. Matrix.
I admire your effort to computerize the problem. I often do this for similar problems, but for the 4 4’s puzzle, I’ve never considered it. I guess I prefer to keep it as a thing to have for thinking about when driving or trying to fall asleep. (Two non-intersecting activities, I hasten to add.)
Comment by John Y. on August 27, 2007
I had not assumed concatenation was legal. The initial statement of the problem says you are to calculate all integers from 0 to 100 using the number 4. Therefore, I thought it more reasonable to assume the postfix expressions to be evaluated were lists of tokens, with each token having one of seven possible values: 4, ‘+’, ‘-‘, ‘*’, ‘/’, ‘R’, and ‘!’.
Personally, I don’t like the idea of introducing operators that can only accept 4s as operands, but in trying to hunt down the “original” or “official” four fours problem, I found a four nines problem (attributed to Dudeney and paraphrased by me below) which was expressed in a way that makes concatenation of nines, and only nines, very clear and palatable:
Due to the context, it makes perfect sense that you should be able to simply put two aluminum 9s next to each other for house 99.
I like the idea of decimals and repeating decimals vastly less than I like the idea of concatenation (I am basically fine with exponentiation). While I do suspect the four fours problem with only the six original operators is insoluble, I would rather change the problem to “How many integers from 0 to 100 can you construct with a postfix expression consisting only of (etc.)?” Or perhaps a bigger range of integers, since 0 to 100 seems to be solved at seventy-something. Or “What is the fewest total number of 4s, coupled with these operations, needed to construct 0 to 100 (or number houses 0 to 100)?” Or how about allowing concatenation as the seventh operation, but make it a standard binary operation: When the concatenation token is encountered in the input, pop two values from the calculation stack, concatenate them, and push the result back onto the stack. Also, Wikipedia states that “most versions” of the four fours problem stipulate that you must use exactly four fours for each integer you are trying to construct.
Comment by Aristotle Pagaltzis on September 1, 2007
Well, in mathematical terms, any “string operation†on numbers is just the same as multiplying by the radix to some power. Concatenation of single digits is just x ∙ b + y, where b is 10 in this problem.
I actually still dislike using concatenation to some extent, because it often requires fudging the exponent of the radix, so it doesn’t ever feel like an axiomatic operation. But the above approach is valuable for making “string operations†mathematically tractable, f.ex. when you have to prove something about numbers whose base n numerals show a particular relationship between particular digits.
(PS.: Julian, if you’re going to have mathematical discussion in comments, it would be very helpful to add
<sup>and<sub>to the list of permitted tags. I rewrote my comment to avoid needing them, but that isn’t always possible.)Comment by Julian on September 2, 2007
Aristotle,
Your wish is my command.
I wrote a quick WordPress plugin that added subscripts and superscripts, lists and definitions. I can’t see any security risks with the tags I’ve added (but I am wondering why they weren’t permitted in WordPress in the first place).
Still no image tags though; I am mulling over what sort of spam that might allow. No tables either, because that will take thinking, and I didn’t have the time at the moment.
Comment by Aristotle Pagaltzis on September 2, 2007
Very nice!
Nit: it says
<ins datetime="" cite="">and<q>; I think you wanted to allow theciteattribute on the latter, not the former.I don’t know why these tags are not permitted on a default install either. I can’t think of any effect either other than discouraging properly structured long comments – surely that’s not a goal? No images is just fine with me, btw, as is no tables. But lists are essential – and they’re allowed now, finally! The current lineup seems pretty complete in terms of common markup; off hand, I can’t think of any tags I might miss.
Comment by Julian on September 2, 2007
I’ve added
citetoqtags. Theciteattribute is allowed oninstags. (Will anyone ever seriously use that tag in a comment? I doubt it!)I would like images permitted in comments – e.g. the Man In The Moon article could have people submitting their own pictures. However, it leaves open the question of who hosts the pictures. Also, if I was a spammer, I would be actively seeking sites that allowed the posting of pictures in comments.
Comment by Julian on September 2, 2007
John,
Your arguments against concatenation and/or the rephrasing of the problem are all valid. It is funny that I just assumed its validity to begin with. It seemed natural to me.
(I didn’t even begin to consider the different bases, as Aristotle suggests.)
I share your distaste for the repeating decimals.
Comment by Julian on September 2, 2007
Aristotle,
A minor consideration when defining concatenation as a simple function – it is a function that only takes digits (or the results of the concatenation function) as an argument. You may not pass the result of another expression to it. This was something minor I had to handle when coding.
Comment by Julian on September 2, 2007
So what ever happened to this program? Well, it appears my software is still buggy, because the 9th cycle (i.e. working out formula that ar 9 digits long) took 2130 times longer than the 8th cycle, rather than the expected 8-10 times longer +/- 50% error bar due to other CPU loads.
I aborted it after the 9th cycle completed, and haven’t got back to it this week to work out what went wrong.
Comment by Katie on July 23, 2008
1=4/4
2=√4
3=√4+(4/4)
4=4
5=4+(4/4)
6=4+√4
7=4+4-(4/4)
8=4+4
9=4+4+(4/4)
10=4+4+√4
Comment by smirg on September 16, 2008
nerds
Comment by POPSTAR5000000 on October 6, 2008
AGHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH help! lol. my teacher set this for my whole class to do as homework
when I went to school not long ago. I just thought that I’d refresh on all of this but there’s so much to remember, and the computer symbols are extremely confusing. I hated that teacher! Anyway I think that Katie’s comment may be wrong, as she doesn’t always use four fours which is the aim of the puzzle. Anyway, have fun working this horrible stuff out. xD
Comment by jennifer on March 31, 2010
11. 4(2)-(4/4+4)
Comment by Julian on March 31, 2010
Jennifer,
Presumably by 4(2) you mean 42, which is not allowed.
44/4=11. (I am not adopting the “exactly four 4s” rule.)
Comment by John Dixon on April 26, 2015
Hi! I just tried out this problem on my YouTube channel, and continued it in a word document on my computer. I looked up the rules, and apparently, they’ve added 2 extra symbols that REALLY help. Along with exponents and the overbar, you can now use percents, AND, you can put a 4 in front of a √ to indicate the “4th root” of a number. Not only that, but you can put a .4 in front of the √, and that means the “.4th root”, which is just raising the number to the 2.5th power. Now I can get 32, 54, 100, and 120 with just 2 fours, and having benchmarks like this has helped me get to where I am now. I’ve gotten to 131 and plan to at least make it to 150.