OddThinking

Introduction

In this article, I describe how I wrote some software to tackle the Slitherlinks puzzles.

From the start, I didn’t attempt to write a “Slitherlinks Solver”. That would take some inelegant brute-force. Instead, I set-out to write a “Slitherlinks Helper”. My goal was to have a tool that would assist with the mundane and obvious elimination tasks, and leave the more complex decisions to the human player.

I had been playing Slitherlinks manually for a while, so I had a number of ideas I wanted to try out. I will describe those ideas here too. In the end, however, not many of them made it into the code.

The Basic Version

Basic Object Model

The architecture I used was my old stand-by, that I have used in many puzzle projects before this.

There were a number of autonomous objects that were responsible for trying to solve their own constraints. The passed messages to their neighbours informing them of their progress.

A “clue box” was one of the cells containing a number. It counted the number of inked, blank and unsolved lines neighbouring it. If the number of inked lines equalled the clue number, it blanked any remaining unsolved lines. If the number of inked lines plus unsolved lines equalled the clue number, it inked in the remaining unsolved lines.

An “intersection” represented the the junction of several lines. (Typically four, but sometimes three or two, on the edges or corners.) It also counted the number of neighbouring inked, blank and unsolved lines, and ensured that they totalled zero or two, using similar rules to the clue box.

A “line” represented a line segment between two intersections. It could be blank, inked or not yet solved. Initially, at least, it had no constraints to check – it would just accept the first value it was given by the clue boxes and intersections.

I recently described the Message-Passing designs that I have used. I re-used an implementation from another puzzle project without touching it. It was a Prioritised Command Set… Well, that’s not entirely true. It was actually Prioritised Command Queue. I must have grabbed it from the wrong directory, and I didn’t look at it very carefully! The result is the same, just a little less efficient. Run-time performance turned out to be quite acceptable without any optimisation, so when I noticed the mistake I didn’t bother fixing it.

Also, I never found the need to override the default priority. All the commands had the same priority! So it was effectively just a Command Queue.

Basic User Interface

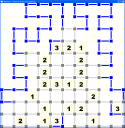
I put a PyGame window in front of the data model, as is my wont. The results were shown in my recent Slitherlinks hints article, but here is a full-sized example, half-solved.

I mentioned above that I had been solving slitherlinks manually for some time. My normal technique was to grab a screen-shot of the PDFs provided by Conceptis Puzzles, load it into Microsoft Paint, and use the line tool to draw blue and yellow lines. (Yellow indicated blank.) That allowed me to switch colours very easily, by dragging with the left or right mouse-button.

When it came to the user interface, it was, therefore, natural for me to translate that into a left-click on a line indicate it should be inked, and right-click indicate it was blank.

User Interface Object model

In previous puzzle solutions, the GameWindow object has reacted to a click operation by doing the maths to converted the pixel co-ordinates into grid co-ordinates, find the appropriate object and call the appropriate method.

This time, I had each clickable object (just the lines, as it turned out) register its bounding box pixel-coordinates. The GameWindow slowly sifted through each bounding box until it found one that contained the pixel that was clicked, and called the appropriate method on the associated object. This is probably less efficient. However, it kept the details of how the object was drawn encapsulated inside the object, rather than spread over two parts of the code. This was prettier.

One day, I will sit still long enough to add a Model-View-Controller pattern. The view and the model are still too tightly coupled at the moment; I have to wade through code about pixels and colours to get to the code that knows about how many lines can join in an intersection.

Basic Implementation: Result So Far

The implementation by no means solved the puzzles by itself. It wouldn’t get close, even with “easy” puzzles. However, it certainly succeeded at its job of helping. It’s not uncommon for large parts of the board to magically solve themselves after a single decision. Slitherlinks puzzles have become much more intense; all the drudgery is dealt with, and only the hard stuff remains.

I found I got a lot better at the higher-level patterns, now that the small ones were being taken care of. For example, this was when my vague thoughts about needing the right number of lines coming into an area gelled into my Jordan Curve theory. (Actually, it’s not a theory but an firmly established hypothesis. One day, I will have to work out how to prove it!)

So, in this way, the basic implementation was a roaring success. stop I have been bashing away at dozens of these puzzles. me Hundreds. somebody It’s been great. pleaaase!

Advanced Concepts

Here are some of the more advanced features that I added, or failed to add, to the basic implementation.

Pattern Recognition

In the Slitherlinks hints and tips article, I describe a number of higher-level patterns that can be recognised to more quickly reason about certain lines. The basic software implementation didn’t attempt to detect them.

I wondered if I should codify these rules in a manner that a pattern-recognizing object could zip over the surface of the puzzle looking for a match (remembering to rotate and flip every pattern in the search!) Having each pattern as one object seeking matches to its own rules sounded cool, but I wasn’t sure that it fit with the rest of the architecture – where objects represent parts of the final solution with constraints to meet, rather than potential solutions seeking a place on the board to land.

Here’s an alternative implementation. Have, for example, a ThreeClueBox object that inherits from ClueBox, constraining its clue number to three. The ThreeClueBox could know about all of the patterns involving threes, and could try to work out if that pattern applied to itself and its neighbours.

Care would need to be taken to divvy up the patterns that involved more than one clue box, so only one rule would trigger.

It might be tricky implementing this without grossly breaking encapsulation. For example, how would you check if your Eastern clue-box neighbour’s Northern line’s Eastern intersection is solved, while trying to avoid looking directly at the data structures involved?

In any case, I never tackled this; there’s a slim, slim chance I will try it one day in the future.

Did I mention the chance was slim?

Curves

I implemented a Curve object late in the process, but it had always been expected. A curve represent a set of connected lines and intersections. Each curve has a unique id number. If two curves get connected together, they are merged and they take the lower id of of the two curves.

One of the rules of Slitherlinks is that there is only one loop (closed curve) in the final solution.

In an unsolved line could connect two intersections connected to the same curve, then it would close the curve, and that would be wrong. Except in one situation – when it is closing the very last curve and solving the puzzle, and only then if all the clues were solved too.

I wrote code to detect the potential closing of a loop. If this is detected, the line is coloured purple.

I originally intended to write some more code that detected whether it would solve the puzzle, and actually ink or blank the line accordingly. I never got around to it; somehow receiving the purple hint was cooler than having it actually resolve the decision.

I did maintain a count of the number of curves remaining and the number of unsolved clues remaining. I declared that the puzzle was solved when there was only one curve and no unsolved clues. Later I realised that it should also insist that the final curve was closed, but this doesn’t make a difference in real puzzles.

I am not happy with my implementation of the curves. I felt, for reasons I feel I cannot defend now, that it wasn’t satisfactory to push a request to resolve the curve status onto the Command Queue. I decided that it couldn’t be deferred, but had to be constantly up-to-date. Otherwise, every time you saw two different-valued intersections, you couldn’t tell if they were on separate curves, or merely hadn’t gotten around to merging yet.

Now, I figure “So what? You’ll get it right next time you visit; just make sure you inform your neighbouring lines/intersections every time you curve number changes.”

The result of this impetuous demand for instant accuracy was that the solution effectively had two message-passing systems. A Command Queue handled most messages, but a simple recursive algorithm handled the curve-merging.

This mishmash was one of the reasons I wrote about Message-Passing designs – to prevent me from making that mistake again.

Despite my unhappiness with the dirty implementation, I was happy that the nebulous concept of “only one loop” that sounds like a global property of the game board, requiring a central controller, could instead be broken down in small, self-contained objects that could, between them, manage this concept.

Clue Boxes with Permutations?

I had assumed that, at some stage, that clue boxes would hold a list of possible line permutations.

For example, consider the “2 in a corner” example from my previous article.

Of the 16 possible combinations of line segments, only six of them match a clue number of 2. Of those six, only two are legal in the above example.

What object is storing this knowledge?

The answer is “None of them”.

It just never came up. There seemed to be no need for it. Perhaps if I had implemented pattern recognition, it might have been useful.

Sourcing Clues

With each puzzle, at some point, the question comes up of where do you get the puzzles from?

One solution is to create your own puzzles, but that’s a whole project in itself.

Another is to type them in by hand from some puzzle source – a task that is both error-prone and laborious.

My slitherlinks puzzles used to arrive in PDF form from Conceptis Puzzles.

An idea I have had for a while (and actually prototyped for Nonogram puzzles) was to grab a screen shot of a puzzle, and use “human-mediated OCR” to read the data.

In this technique, the computer looks at a bit-map representing the screen-shot, and scans for long horizontal and vertical lines. It then computes the size of the grid, and is thus able to calculate the bounding box of the numbers.

It uses a hash of the numbered bitmap to look up the corresponding number in a dictionary. If it isn’t present (as it won’t be, the first time) it presents the tiny bitmap to the user and asks them to parse it as a number. The result is stored in the dictionary, persistently. At first, it is almost useless, but before long it has a big enough dictionary to handle most of the numbers in the puzzle.

In the end, I didn’t do that for this puzzle, as I found Slither Link Cosmos (a partly Japanese site, but obvious from context) had a web-site format that was rather easily scrapeable.

Yes, my copyright-violation senses are tingling. However, there aren’t any obvious forms of income that I am circumventing. I would have to ask permission before sharing that code. In the meantime, I am enjoying their generosity of over 700 free puzzles.

Hypothetical Hypotheses

This is a concept that I have been meaning to try out for a while.

When I solve a puzzle like Slitherlinks, I sometimes have to degenerate into trial-and-error. I normally choose a different set of colours to draw with, and try to find a “tipping point” where a small change leads to a cascade. I make an arbitrary choice and follow it to the conclusion – either solving the puzzle, getting stuck again, or leading to a contradiction. If I get a contradiction, I erase the hypothetical, invert the starting line, and move on.

I wanted to support that user behaviour.

The Nikoli implementation of Slitherlinks has a “try” mode, which allows you to tentative mark some lines, and then commit or abandon them.

My idea works differently. There’s a new object called a Hypothesis. (I know it should be called Conjecture – let it go.) It contains a unique symbol, and a list of affected objects.

When you create a new hypothesis, it is associated with a particular decision. For example, in Slitherlinks that might be setting a line to inked. The appropriate object is sent a message saying it is set to inked in the context of a specific hypothesis.

If an object sees a hypothesis it hasn’t seen before, it registers itself with the hypothesis. It creates a clone of its data, stored in a dictionary indexed by the hypothesis id. It then attempts to solve the cloned data – passing the hypothesis id around with all the messages.

If the puzzle is solved, in the context of the hypothesis, the hypothesis is confirmed.

If the puzzle leads to a contradiction, the object rejects the hypothesis. The hypothesis object then informs all of the affected objects to delete that conjecture. The original decision that started the hypothesis is eliminated from consideration (which itself may lead to some progress in the puzzle).

The most likely outcome is that the hypothesis leads to some progress, but no real decisive outcome. The hypothesis could be deleted without an outcome at that point, or, most likely, just ignored, just sitting around wasting a little memory.

Here’s the tricky bit. Hypotheses are arranged in a tree structure – each hypothesis has a base hypothesis. Any progress on the base hypothesis is automatically applied to all of its children hypothesis. At the top of the tree is “reality” – the final set of known truths that we began with.

When an object sees a new hypothesis, it clones data from the nearest base hypothesis that it has.

A base hypothesis may independently derive a firm confirmation about the same fact that a hypothesis object was tentatively investigating. If so, the hypothesis can be confirmed. Alternatively, it may deduce the opposite fact about any of the hypothesis’s conclusions, in which case the hypothesis can be rejected. In this way, those lazy, half-finished hypotheses sitting in memory can prove to be become useful or get eliminated.

Now, this may sound a lot like evil back-tracking. Indeed, that is exactly what it is. However, it is limited to user-driven hypotheses – assisting the user in the “what if?” tasks they normally perform – rather than mere brute-force. It hasn’t escaped me that, during the quiet cycles, the software could make random conjectures, just on a whim to see if it helps. Banish that thought!

In order to implement this functionality, my first task was to change the way the software behaved when it encountered a contradiction to the rules – i.e. 3 lines adjacent to a 2 clue box. Originally, it aborted with an assert failure. I changed the Intersection and Line objects to have an error state which they would enter upon finding a constraint had been violated. They turned red in this circumstance.

Then, I had an idea for a quick hack. As a prototype step towards the full Hypothesis implementation, I would hack together a rather ugly Undo function. Every user action was stored in a command history. If the user selected Undo, then the entire gameboard was discarded, a fresh one created, and all of the users commands (bar the last one) were replayed. Ugly. Inefficient. Very quick to implement and very effective.

The result of having an undo operation was interesting. It almost destroyed the game play! Before undo, when the going got tough, I would have to start concentrating to work out consequences. Now, if I am not diligent, I degenerate into “Oh, I dunno. What happens if I set this one? Oh, a contradiction? Whatever. Undo and set it to the opposite!”

The Undo operation gets clumsy if you need to undo more than a couple of steps. The full Hypothesis implementation would solve that. However, I abandoned the Hypothesis implementation; it would devolve into just keeping track of my random clicks.

Conclusion

I didn’t exercise every technical trick I hoped to try out, but this was the most fun outcome of the puzzle-solvers – until I broke it by adding Undo.