OddThinking

You’ve all probably heard of the Golden Ratio or the Golden Rectangle, which has sides in proportion to the Golden Ratio.

The remarkable mathematical property a Golden Rectangle has is that its long side divided by its shortest side is exactly equal to the ratio of the number of bullshit claims about the Golden Rectangles compared to truthful ones.

Sure the Golden Ratio is a real thing. It is useful for producing spirals, ISO-standard paper sizes [Stop Press: I WAS WRONG! See comments], and interesting mathematical puzzles.

But the claims that it is some biological ideal of beauty or perfect design seems like unjustified crap to me.

What evidence is provided?

That ancient architects have used it to design buildings. Maybe. So? How would you prove that if they made them just a little bit wider they would be any less beloved?

That some pretty faces can have spirals and golden rectangles drawn on them? Every time I have seen such examples, the lines on the rectangles cross up in completely arbitrary points on the face. If you used a ratio of 1.6, or 1.8 or 2.0 you could also get similar results from pretty faces – especially if you are permitted to select your own faces for the experiment.

The result is we get designers constraining themselves to arbitrary rules, and then feeling proud that they did so.

What triggered this rant?

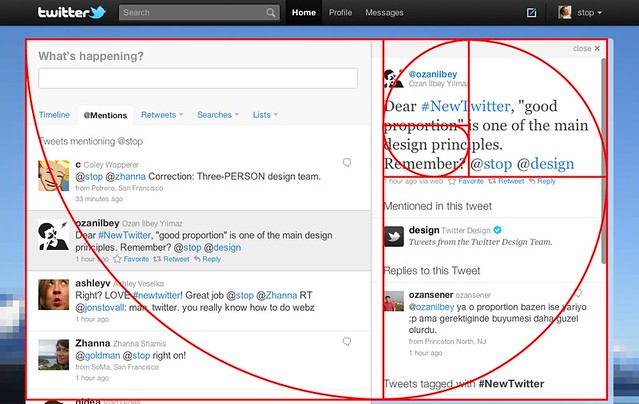
The New Twitter design team claim they were influenced by the Golden Ratio (except if you have a browser window that is larger than the minimum, of course.)

Pretty, right?

Lets look at the claim closer. The spiral starts at the top left corner, and touches the bottom surface at the division between the left and right panes…. Wait, no it doesn’t. The right-hand pane is too wide.

Then it extends touch the right-hand-side at the bottom of the top right pane. But wait, where is the bottom of the top-right pane. Is it the bottom of the word “Remember”? The top of the words “1 hour ago”? The bottom of the words “1 hour ago”? The top of the words “Mentioned in this tweet”? How is my eye supposed to know which they arbitrarily decided when Twitter made the design? Should I even believe it was ever considered by the team, and not just arbitrarily claimed later?

Then the spiral touches the top of the screen at the point that lines up with… um.. nothing in particular.

Then it keeps going to touch halfway through the word “proportion” for no reason. Why is the spiral still being drawn?

But no, it keeps going to touch under the gap between “m” and “b” in “remember”, which is beautiful. Then it pushes right past the “i” in “principles”, which is surely some sort of metaphor. Finally, it stops in the middle of the “n” in “proportion”, which is surely some form of ideal point, justified by the ancient Greeks.

Also note:

• the left column is extends longer than what is shown
• the right column appears to be truncated (there is no content under the heading “Tweets tagged with #NewTwitter”
• I suspect the other content on the right is actually dynamic in size, so the ratio won’t apply when it becomes smaller or larger
• the “close” button should take up a majority of the top right pane, in order to properly follow the ratio.

This entire claim that the Twitter design follows the Golden Ratio is completely bogus. I don’t know if they really did try to use the ratio, but I see no evidence that they succeeded, and I hate that they have set up in the minds of the next set of designers that such a constraint is a good idea to improve user opinions.