This is an analysis – and a proof of cryptographic weakness – of a master/slave-like selection protocol that has been embedded into a number of playground games.
To decide who is “it” (or “in”) first, in a playground game, such as chasey (a.k.a. tag), a fixed algorithmic process is used to make a pseudo-random choice.
The players stand in a circle, and one self-selected player (a.k.a. “bossy-boots”) starts on the left and points to each player one at a time, clockwise, while reciting a traditional rhyme whose original meaning has been lost.
Ip dip dog shit, you are not it.
Of course, this is a deterministic procedure, and we can, with diligence, careful calculation, computational power and just a little bit of luck, reverse engineer the algorithm and determine who will be eventually selected.
Let the n players be labelled 0..n-1, where the first indicated player (i.e. “Ip”) is player 0, and n >= 2.
Define out(n) as the player who is immediately eliminated, for n >= 2.
Note the verse has eight words. The player pointed to on the eighth syllable (i.e.(8 - 1) mod n) is eliminated.
So, out(n): (8 - 1) mod n
In the simplest case, note out(2) = 1. That is, the player who is not initially pointed at is out.
Define in(n) as the player who is eventually selected, for n >=2.
Again, in the simplest case, in(2) = 0. The player who is initially pointed at is in.
For larger n, the process is to eliminate the out player, and then restart the numbering from the player to the out player’s left, with one less person.
Counting from the outed player’s perspective, the player to their left is player 0 (for the subsequent round), and the player that is eventually selected is in(n-1). Changing the point-of-reference to the initial positions, the player that is eventually selected is out(n)+in(n-1) mod n.
That is:
in(n): 0, if n=2. out(n)+in(n-1) mod n, for n>2.
School-children should keep that recursive function in mind when deciding where to stand compared to the bossy counter.
A follow-up question becomes “When is it favourable to step up, and self-nominate as ‘bossy-boots’?”
Define is_bossy_in(n) as true, if the person starting the count-off is in, else false.
Now, the count traditionally starts to the left of the bossy-boots, so the position of the bossy-boots is n-1.
Thus, is_bossy_in(n): in(n) == n-1
In practice, is_bossy_in(n) is true only for n=3, 13, 15 and 26. No other value for n < 1000 has been discovered by researchers.
Thus, players wishing to game the system by avoiding being it can (after quickly checking n is not a member of a small set) nominate themselves as bossy-boots and avoid detection by visible counting positions or unseemly, last-minute scrambles.
Here is a chart of precalculated values (presented as an image because of a WordPress bug, which is also affecting formatting below... weird.)
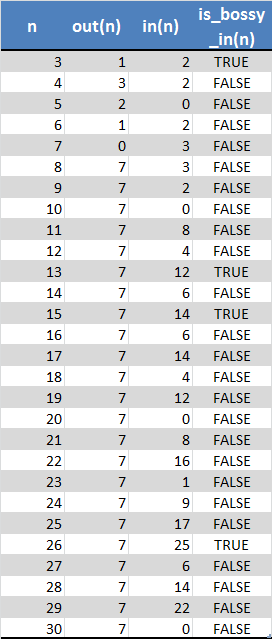
It is expected that trivial modifications to the rhyme, such as “Ip dip dog shit, Fucking bastard dirty git, You are not it.” sometimes used in the older schools or any of the “Eeny, meeny, miny, moe” variations will have similar vulnerabilities, despite approximately doubling the bits-depth of the encryption. The definition of out(n) just needs to have the appropriate word count (or syllable count, depending on the counting scheme) substituted in, and the calculations re-run.
Further research is required into the apparent bias against the initial position, and relative safeness of the odd positions.
Note: Disclosure of the security vulnerabilities in this game was done responsibly, by informing a school teacher of the risks. After a reasonable period without action taken, it was determined that full publication was in the public interest.
Comment by Sunny Kalsi on April 22, 2013
Little known fact: That poet was Banjo Patterson.
And now to go edit Wikipedia… for unrelated reasons.