OddThinking

[*FX*: Sound of man blowing dust off and old engine, opening the fuel valve, adjusting the throttle and then yanking the pull cord a couple of times until the motor starts up.]

Would you look at that? The blog still works.

I’ve come back for a couple of quick posts. I used to document all my attempts at using a Puzzle Solving Framework. I may as well keep it up-to-date with developments.

Introducing the Snail puzzle

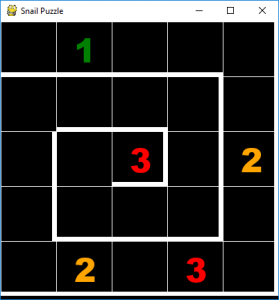
Two months ago, I decided I wanted to tackle the Snail puzzle (which I found in 100 Logic Games).

The gameboard is a grid of squares, which are marked out as a spiral. Each cell can marked as “empty” with a dot, or marked as having a 1, 2, or 3 in it. Some are filled in as initial clues.

The rules are are:

• Each number must appear exactly once in each row and column.
• As you follow the spiralling path from the outside to the centre, the numbers must repeat the sequence 1-2-3, starting with a 1 and finishing with a 3.

Solving the Snail

I implemented this a few months ago, so I am a little vague about my motivations.

I recall I had some ideas about adopting a different approach than normal. I was considering trying a more brute-force method, because I thought I could model the problem in a way that the number of combinations to try was very small (i.e. in the millions).

When I did the maths, it didn’t scale well. The 5×5 puzzle above could be solved quickly, but an 11×11 was infeasible.

So, I used my tried-and-true technique of the framework I wrote all those years ago.

I had another hypothesis that a couple of simple logical inference rules might be sufficient to solve the puzzles, if I modelled it right.

In particular, I didn’t model each cell as having one of four values, but as having one of six values: 1, 2, 3, ●1, ●2, ●3.

The three dotted values were displayed as a single dot (i.e. an empty cell), but behind the scenes the rules were more complex. A ●1 cell could only be followed by a 1 cell or another ●1 cell. A 1 cell could only be followed by a 2 cell, or a ●2 cell. This allowed information about what the last cell was to be carried around the corners.

It seemed to work. A implemented those constraints, plus the typical exactly-one-number-per-row exclusion rules – i.e. if there is a 3 in this row, no other cell in this row can be a 3. If no other cell *might* be a 3 in this row, this cell must be a three.

Those rules were sufficient to solve most of the puzzles I sampled.

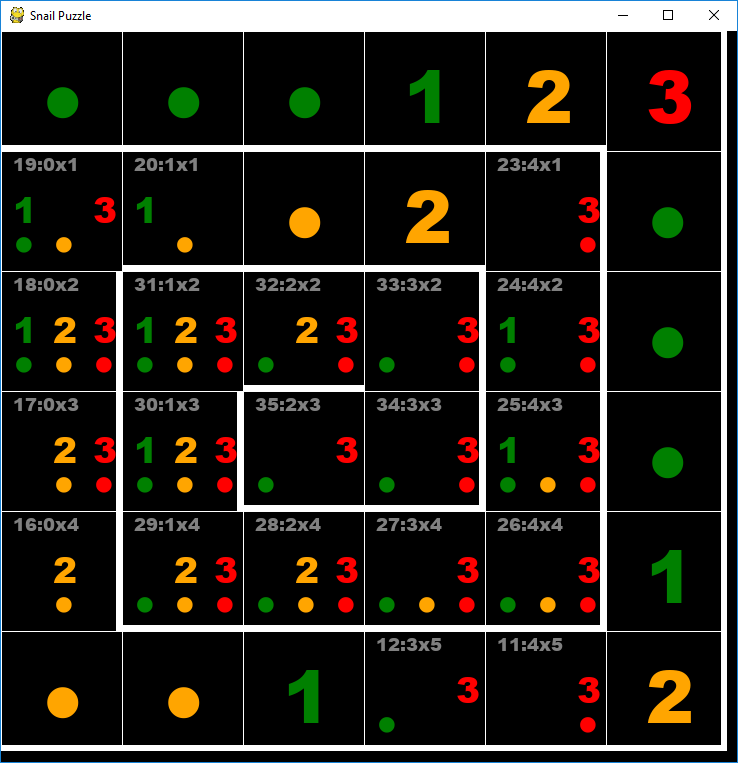
However, some puzzles didn’t succumb to these rules. Here is a game that the software got stuck on:

The small grey numbers describe the cell’s address (position in the spiral and grid co-ordinates) The small colourful numbers and dots represent the internal state of the cells – legal options that the software han’t been able to eliminate.

Look at cells 24 and 25. One of those must be a 1, so until a 2 is encountered, there can be no 3. So, we can eliminate the 3 option from calls 25, 26, 27 and 28. If you do so, the solver can take over from there and complete the puzzle.

The complexity of the next level of logic to detect situations like this made it seem too brute-force for me to consider implementing it.

I left it there.