Something has been bugging me since I posted the red laser pointers plus moon = red eclipse idea.
It’s not that it is morally wrong.
It’s not that it is astronomically wrong.
What’s been bugging me is the need for a back-of-a-really-big-envelope calculation…. just how many laser pointers would it take to fake a red eclipse?
Let me fill that gap now.
Part 1: What’s the cross-section of the moon?
Approximation: The moon is a perfect sphere.
The cross-section of the moon is a circle of area π×R2, where R=radius of the moon.
Fact: The moon has a diameter of 3474 kilometres, which is 3.47 × 106 metres.
Thus, the cross section of the moon is π × ((3.47 × 106)/2)2) = 9.4 × 1012 m2.
Part 2: How much sunlight falls per square metre on the moon?
Approximation: The moon is equidistant from the Sun as the Earth is, and thus the Sun’s radiation on the top of the Earth’s atmosphere is the same as the sun’s radiation on the top of the moon’s atmosphere.
Approximation: The moon has no atmosphere.
Fact: The Solar Constant (total energy in all solar electromagnetic radiation at the top of the Earth’s atmosphere) averages 1366 W.m-2.
Part 3: How much sunlight falls on the moon?
Total energy due to sunlight = Energy per square metre × cross-section area
= 1366 W.m-2 × 9.4 × 1012 m2
= 1.3 × 1016 watts.
We don’t need all of this energy, though, to light up the moon. The red eclipse wasn’t as bright as a full moon.
Part 4: How much of that energy fell on the moon during the red eclipse?
To start with, the red eclipse only had the red wavelengths.
Approximation: The Earth’s atmosphere absorbed all of the visible spectrum except the red range (between about 625 nm and 740 nm), and it attenuated the red range by 50%.
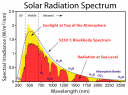
How much of the sunlight’s energy is in the red wavelengths? Well, this is described in the following chart (from Robert A. Rohde, via Wikipedia).
So the red light is the area under the curve in the red part of the spectrum.
Oh dear, how do you find the area under a curve?
There are two ways:
One is to find the integral of the function. That only requires two items that I don’t have: a description of the function, and any recollection of how to integrate.
The other is the old-fashioned way – draw the curve on a grid and count the squares underneath it.
Here we go then:
First, we colour the graph into red and non-red areas.
Approximation: The red area of the graph reasonably represents the wavelengths associated with the red hue of the eclipse.
Then we run a simple Python based on the Python Imaging Library (PIL) script:
Approximation: That the pixels in the mock-up curve accurately represent the area under the real curve.
>> import Image
>> Image.open("red_sunlight_graph.png").getcolors()
[(522179, (255, 255, 255)), (6516, (238, 3, 17)), (57505, (3, 64, 238))]
This means the total energy arriving at the moon is (6516+57505) pixel units, while the total red energy is 6516 pixel units, or just over 10%. Remembering to attenuate by 50%, we get only 5% of the solar energy making it past the Earth’s atmosphere.
Total red light energy we need to transmit to the moon: 1.3 × 1016 watts × 5% = 6.6 × 1014
Part 5: How much power does a laser pointer emit?
According to the UK Health Protection Authority’s advice on laser pointers, laser pointers should have less than 1 milliwatt of power. Wikipedia claims a five milliwatt maximum in the USA, but a citation is needed.
Approximation: Laser pointers are 10-3 watts.
Part 6: So, how many laser pointers does it take to change a moon?
First, we need a few more rather coarse approximations that under-estimate the real number of lasers required :
Approximation: The Earth’s atmosphere does not attenuate red laser light – there is no Raleigh scattering or dust in the air.
Approximation: The laser beam is completely parallel, and does not diverge, even over the average distance of 384,000 kilometres between the Earth and moon.
Total power required divided by power per laser = 6.6 × 1014 watts / 1 × 10-3 watts = 6.6 × 1017.
We have an answer! Two-thirds of a quintillion lasers: 660,000,000,000,000,000.
Everybody on Earth (except the astronomers, of course) will need to carry 100 million laser pointers each.
That’s almost as many lasers as kernels of wheat that have ever produced.
I guess what I am saying is, we’ve got a lot of work ahead of us in the next few weeks, if we want to pull off this little prank – we’d better get started soon!
Comment by Chris on September 1, 2007
I think I’ve found a hole in your otherwise air-tight logic. If this is a prank on astronomers, and we’re getting everyone on Earth to participate… err…
Anyway, you need to factor USAF’s fleet of Directed Energy Sea Mammals and their 750kW solid state lasers. That’s 750,000,000 fewer lasers we need per DESM, or about 7.5 astronomers.
Comment by Julian on September 1, 2007
Chris,
I considered this issue, of course, but I didn’t have room to include it in the initial presentation.
Let me give you a few more digits of precision to explain.
Number of lasers required: 6.58924E+14
Population of the Earth: 6,615,374,108
100 million laser pointers each, will leave a total of 26,100,000 people not carrying any lasers. That should cover all of the world’s astronomers as well as any astro-sympathisers that we can’t trust not to blab.
Early reports suggest that there are correlations between cetaceanism and astro-sympathification, which is why I discarded the DESM concept initially. A high-quality vetting program may allow us to re-consider this decision.
Comment by John Y. on September 1, 2007
Fun analysis, and much more involved (but probably more accurate) than I had expected when I read the title. What I thought you were going to do was estimate the area of a laser pointer’s dot, and then divide the area to be covered by the area of the dot to come up with the number of pointers needed.
I hadn’t really thought it through. For example, I know lasers are supposed to have ridiculously low divergence, but what if the beam from a consumer-grade laser pointer spreads out measurably? Then you’d need to measure dot size at a couple distances and extrapolate. If one pointer illuminates, say, a square centimeter of visible Moon, you’d need only about a seventh of your estimate. But it’s pretty far to the Moon, and I have no idea how coherent these lasers are. For all I know it could have spread to a square meter by then, or even more.
Comment by Sunny Kalsi on September 1, 2007
John: I don’t think the coherence of the lasers matters. If a laser is spread out twice as much as an ordinary laser, you’ll need two lasers on that same point to have the same brightness (AFAICS).
Julian: I think you’re vastly overestimating the brightness of the moon. A lot of people watching the moon during the eclipse said that the “dark part” of the moon was practically black until the bright parts were completely gone. Our eyes have a very high dynamic range, and even then they were completely saturated by the brightness of the moon by direct sunlight. That is, unless the moon’s redness got brighter after the direct sunlight was gone.
Comment by Julian on September 1, 2007
John,
A single dot of one laser isn’t going to be bright enough to be visible when it is reflected back to Earth. Each point on the moon is going to need more than one laser pointer to hit it to get enough photons bouncing back.
My original plan was to find out the albedo of the moon (about 12%, as it happens) and try to work out how bright the moon had to be to be visible to the naked eye, so I could work out the energy required, but I decided it was easier to go the other way – work out how much light was hitting the moon from the Sun in the first place.
If the dot has spread to a square metre, my estimates still hold – there’s just lots of overlap.
The reason I added the approximation that lasers are parallel is that I feared that the dot might have grown to be much larger than one square metre. If, in fact, the laser dot grows to more than the surface of the moon, we will have inefficiency due to light being lost to outer space.
More back-of-the-envelope calculations – if the spread is more than 2 × arctan( (moon radius) / (moon-Earth distance) ), or 0.26° then this will happen. (Calculating this properly – in steradians – is an exercise left to the reader.)
Like I said – this problem was really bugging me!
Comment by John Y. on September 2, 2007
Sunny and Julian,
I realize one laser pointer isn’t that bright. Maybe I’m not either, but I would like to make clear that I never thought one laser pointer dot per dot-area of Moon surface would be sufficient to be visible from Earth. But when I initially read the title, I did not know how serious the calculation was going to be. My proposal was a purposely naive lower bound, both in terms of accuracy of the model and number of pointers required.
I think Julian picked a reasonable model, but surely other bloggers (or even Julian himself, in a more particular or long-winded mood) would have been much more meticulous. It’s a judgment call what assumptions and approximations are suitable to make for a blog entry and what is really going overboard. The point of my first comment was simply that I had initially thought Julian was going to use a much smaller envelope.
Comment by Alastair on September 2, 2007
Dan reckons that “if you need less than one millimetre per metre divergence, a diode laser is not for you”. Even the wierd high-power green laser he was testing still showed 1.1-1.2 meters divergence at a kilometer, and goes on to talk about it at great length.
So if we use 350,000km as the distance from the earth’s surface to the moon’s surface, this makes the beams 385km across. Or about 1/10th of its diameter. So divergence wont be a problem.
Comment by Julian on September 2, 2007
Okay, let’s use Alastair’s calculation on the back of John’s envelope.
One dot is 385km across. Assuming it is a circle, that is an area of 1.1 × 1011 m2.
The cross section of the moon was 9.5 × 1011 m2.
So, ignoring the issues of optimal packing, only 81 laser pointers are required to completely cover the moon – that is, to ensure that any point of the moon has a chance of a red photon hitting it from a laser.
Comment by Julian on September 2, 2007
One more issue to consider, when setting up this experiment. The moon is about 1.2 light seconds away. Remember when you adjust the position of your laser pointer to cover a different point of the moon, it will take 2.4 seconds before the change will be visible.
Comment by Jonathon Duerig on September 3, 2007
One issue that is not even considered here is that at most half of the earth has a direct line of sight to the moon at any given time. So if you had the cooperation of a large number of people in Asia and Australia, perhaps it would work locally. But for people like me sitting on the other side of the world, it wouldn’t be noticed. This also means of course that each person would need even more lasers…
Comment by Julian on September 3, 2007
Jonathon,
I just slapped my hand to my forehead in dismay. How could I forget about that?
We’ll need to pick a time where exactly half of the world’s population are at night, and have 200 million laser pointers each.
There’s a plus side though! We just need to ship those laser pointers to the other side of the world, and we can repeat the prank on the astronomers who haven’t seen it yet!
Comment by Andrew on September 6, 2007
I think your calculation is a huge overestimate. The light that falls on the moon during a lunar eclipse is all going through earth’s atmosphere – light hitting earth is blocked, light not hitting atmosphere isn’t bent back.
So the light hitting the moon is limited to that hitting the atmosphere halo of the earth – about 2 * pi * 6000km * 100km (circumference of earth times depth of atmosphere). We’re down to 3.7 x 10^9 already, and that ignores all the light that’s directed the wrong way (outwards, or not scattered, or inwards but missing – since the moon’s area is smaller than earth’s by a factor of 12 or so).
Now you need to figure out what the scatter pattern looks like and… um.. this margin is too small to contain the calculation.
You’re probably down to something more like a million laser pens.
Comment by Julian on September 6, 2007
I’m too upset to consider Andrew’s probably quite valid objections.
I mentioned this idea to a friend, who said she had already heard it from another friend, who in turn said it’s an old idea!
I am distraught. Innovation sucks.
Comment by John Y. on September 8, 2007
You even cited the trouble with the Web in that post about how to suitably capitalize on the eclipse, the predecessor to your simulate-an-eclipse-with-laser-pointers idea. How thoroughly demoralizing.
(That was meant to be sympathetic, but somehow it probably comes across as rubbing it in.)
Comment by Don Davis on June 28, 2009
I have given this matter some thought. The recent proliferation of green lasers of high wattage may invite reconsideration of the possibility of a mass attempt to illuminate the night side of the Moon. I have seen 5 watt green lasers at Burning Man, and many hand held units are now of a power to invite contributing to such an effort. Each laser would have to be aimed precisely enough to hit the dark portion of a crescent Moon, including from daylight locations with the Moon in the sky. The presence of extra lighting on the Moon would best be shown by the beams doing a 10 second off/10 second on pattern with the on and off times coordinated as closely as possible, within a second. All participants would have to be listening to time signals in order to coordinate the timing of ‘pulses’. The nature of the Lunar surface is an unexpected aid to such efforts as glass spheroids are a major part of the surface materials, reflecting light back at the source as does a scotchlite painted road sign. ‘Painting the moon’ may be an uphill battle but the problem is worth reconsidering based on the back scattering property of the Moon and the proliferation of commercially available large green lasers.
Don
Comment by Julian on September 25, 2012
XKCD just came to the table, 5 years too late.